Given that xyz= 1, You will get minimum value only when x=y=z So in this given case, you will get minimum value of x^2y^2z^2 when x=y=z= 1/3 So minimum valueTo ask any doubt in Math download Doubtnut https//googl/s0kUoeQuestion If 2^x = 3^y =12^z show that 1/z= 1/y2/xXyz=2, 2x2y2z=4, xy=2 Extended Keyboard;
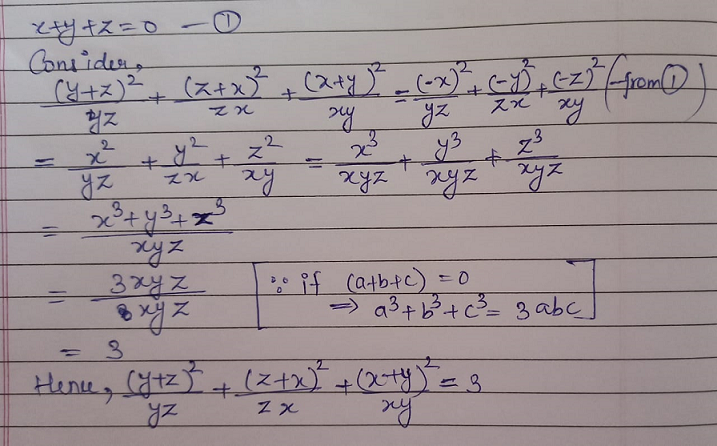
How To Solve If X Y Z 0 Find The Value Of Y Z 2 Yz Z X 2 Zx X Y 2 Xy Mathematics Topperlearning Com 7bcu50oo
F(x y z)=x^2 y^2 z^2 x y z=12
F(x y z)=x^2 y^2 z^2 x y z=12-The Roman surface or Steiner surface is a selfintersecting mapping of the real projective plane into threedimensional space, with an unusually high degree of symmetry This mapping is not an immersion of the projective plane;Show that the intersections of this surface with planes perpendicular to the xand yaxes are hyperbolas Hint Set either y = c or x = c for some constant c The other type is the hyperboloid of two sheets, and it is illustrated by the graph of x 2 y 2 z 2 = 1, shown below
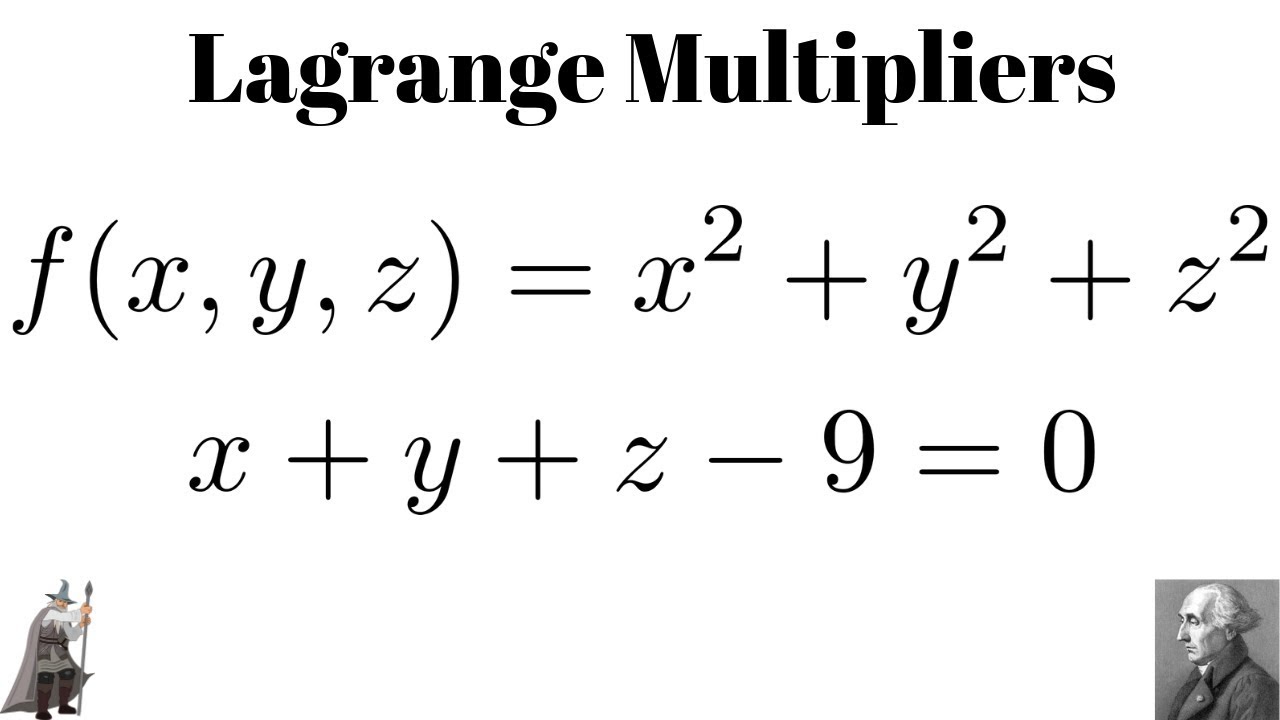


Lagrange Multipliers Minimum Of F X Y Z X 2 Y 2 Z 2 Subject To X Y Z 9 0 Youtube
S is defined as a sphere · $(xyz)(x^2y^2z^2)=x^2y^2z^2x^2yx^2zxy^2y^2zxz^2yz^2=2$ buradan da $3(x^2y^2z^2x^2yx^2zxy^2y^2zxz^2yz^2)=6$ denklemi elde edilir Denklemleri taraf tarafa çıkarırsakLetf (x,y,z) = x^2y^2z^2 Calculate the gradient of f Calculate ∫_C (F dr ) where F (x,y,z)= (x,y,z) and C is the curve parametrized by r (t)= (3cos^3 (t),
1217 · how can i draw graph of z^2=x^2y^2 on matlab Learn more about surface MATLAB C/C Graphics LibraryX y z = 16 x z = 12 y = 2 Log On Algebra Matrices, determinant, Cramer rule Section Solvers Solvers Lessons Lessons Answers archive Answers Click here to see ALL problems on Matricesanddetermiminant;However, the figure resulting from removing six singular points is one Its name arises because it was discovered by Jakob Steiner when he was in Rome in 1844 The simplest construction is as the image of a sphere centered at the origin under the map f
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor0118 · See below Making m = xy n = yz p = xz we have m^2n^2p^2 = 2(x^2y^2z^2x*yx*zy*z) then x^2y^2z^2x*yx*zy*z = 1/2((xy)^2(yz)^2(xz)^2)This equation is in standard form ax2 bx c = 0 Substitute 1 for a, −x−z for b, and x2 z2 −zx for c in the quadratic formula, 2a−b± b2−4ac y=\frac {\left (xz\right)±\sqrt {\left (xz\right)^ {2}4\left (x^ {2}xzz^ {2}\right)}} {2} y = 2−(−x − z) ± (−x − z)2 − 4(x2 − xz z 2) Square xz



Use Stokes Theorem To Evaluate 5 Curl F Ds F X Y Z X 2z 2i Y 2z 2j Xyzk S Is The Part Of The Paraboloid Z X 2 Y 2 That Lies Inside The Cylinder X 2 Y 2 4



Ex 3 2 12 Given 3 X Y Z W X 6 1 2w 4 X Y Z W 3
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutritionThe idea is that since xyz is cubic, it will be larger than x 2 y 2 z 2 unless one number is much larger than the others But if that's the case, we can always replace the largest number with a smaller one (until x,y,z form an acute triangle)Suppose f(x,y,z)=1/(sqrt(x^2y^2z^2)) and W is the bottom half of a sphere of radius 6 Enter ρ as rho, ϕ as phi, and θ as theta What are the integrated integral and limits of integration using spherical coordinates?



Let Math X 2 Y Z Y 2 Z X Z 2 X Y Math What Is The Value Of Math Frac 1 1 X Frac 1 1 Y Frac 1 1 Z Math Quora
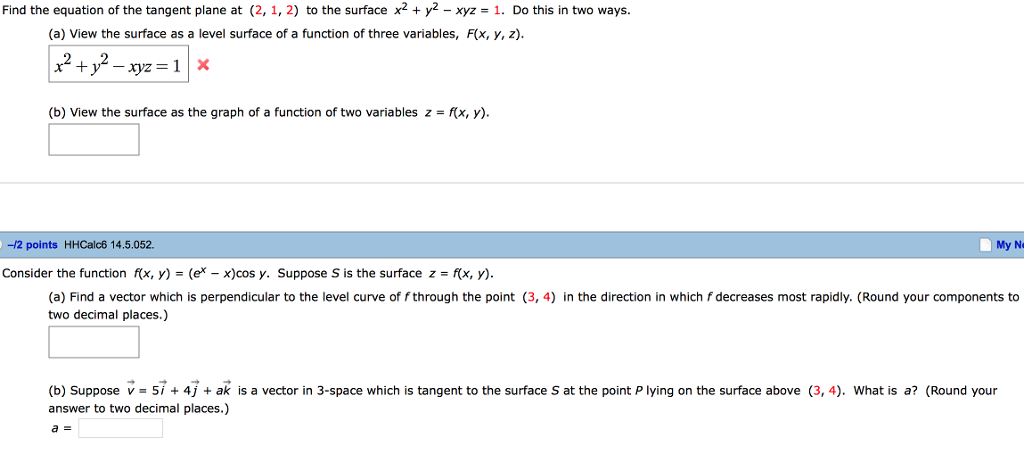


Solved Find The Equation Of The Tangent Plane At 2 1 2 Chegg Com
· 3Dplot of "x^2y^2z^2=1" Learn more about isosurface;En este video encontrarás la solución, paso a paso, del sistema de dos ecuaciones de primer grado, o lineales, con dos incógnitas "1) xyz=12 2) 2xyz=7 En este video encontrarás laIf U = F ( Y − X X Y , Z − X X Z ) , Show that X 2 ∂ U ∂ X Y 2 ∂ U ∂ Y Z 2 ∂ U ∂ Z = 0 University of Mumbai BE Automobile Engineering Semester 1 (FE First Year) Question Papers 141 Important Solutions 525 Question Bank Solutions 527 Concept Notes 24 Time Tables 23 Syllabus



Solved Finding An Equation Of A Tangent Plane In Exercise Chegg Com



Let Math X 2 Y Z Y 2 Z X Z 2 X Y Math What Is The Value Of Math Frac 1 1 X Frac 1 1 Y Frac 1 1 Z Math Quora
2x0 d dx z2 2 x 0 d d x z 2 Since z2 z 2 is constant with respect to x x, the derivative of z2 z 2 with respect to x x is 0 0 2x0 0 2 x 0 0 Combine terms Tap for more steps Add 2 x 2 x and 0 0 2 x 0 2 x 0 Add 2 x 2 x and 0 0 2 x 2 x · Verify Stokes theorem for F =(y^2 x^2 x^2)i (z^2 x^2 y^2)j (x^2 y^2 z^2)k over the portion of the surface x^2 y^2 2ax az = 0 While evaluating the integral we get hard to evaluate integrals What can we do to simplify this?Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 2xy=2;xyz=2;5x2y5z=6 Tiger Algebra Solver
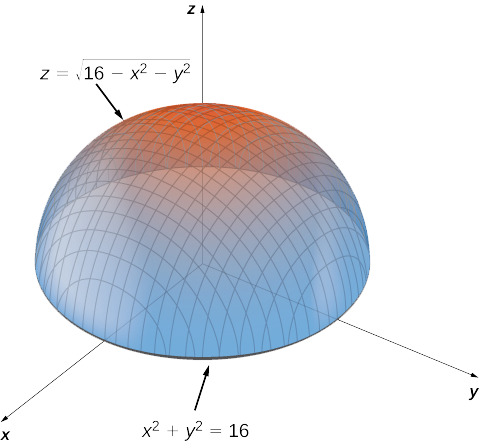


13 7 Extreme Values And Saddle Points Mathematics Libretexts



X Y Z Belong To R X Y Z 4 X 2 Y 2 Z 2 6 Find Maximum Possible Value Of Z Mathematics Topperlearning Com 2j1z7sww
· Once we find these, we can construct any symmetric polynomial in x, y and z We are given x y z, so we just need to derive the other two Note that 2(xy yz zx) = (x y z)2 −(x2 y2 z2) = − 1 So xy yz zx = − 1 2 Note that 6xyz = (x y z)3 −3(x y z)(x2 y2 z2) 2(x3 y3 z3) = 1 SoAnd then now we are given the constraints Um, X plus two I was three z equal six and expose three way place nine z is equal to nine So we are gonna be using equation to for this problem that is given in the book for those problems that have two constraints and that says we want to solve the greeting of f is equal to land The times the grating of G one plus mu times the Grady int g tooMinimize f(x, y, z) = x^2 y^2 z^2 subject to 4x^2 2y^2 z^2 = 4 Maximum Valua At (,,) (1 pt) Find the coordinates of the point (x, y, z) on the plane z = 2 x 2 y 3 which is closest to the origin x = 2 y = z =


If A X B B Y C C Z A What Is Xyz Quora



Applications Of Partial Derivatives Calculus 3
Click here👆to get an answer to your question ️ If f(x,y,z) = x^2/a^2 y^2/b^2 z^2/c^2 1 , then Σ x∂f/∂x is equal toX 2 y 2 z 2 = 1 < Helicóide (*) x = u cos v, y = u sen v, z = v < Catenóide (*) x = cosh v cos u, y = cosh v sen u, z = v < "Mola" (*) x = (11 2 cos u ) cos v, y = (11 2 cos u ) sen v, z = 2 sen u v < Gráfico da função (*) z = sen(x)cos(y)/5 3 cos(7W/4) exp(W)/2 onde W= (x p) 2 (y p) 2F1(x,y,z) = x^2 y^2 z^2 −1 = 0 f2(x, y, z) = 2x^2 y^2 − 4z = 0 f3(x,y,z) = 3x^2 −4yz^2 = 0 This system can be concisely represented as F(x) = 0, where F(x) = (f1, f2, f3)T , x=(x,y,z)T and 0 = (0,0,0)T (transpose written because these should be column vectors) Using matlab
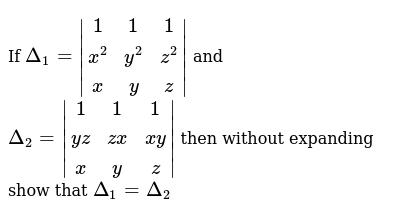


If Delta 1 1 1 1 X 2 Y 2 Z 2 X Y Z And Delta 2 1


Solved Calculate S F X Y Z Ds Sf X Y Z Dsfor Y 3z 2 0x Z6 F X Y Z Z Y 3z2 0x Z6 F X Y Z Z S F X Y Z Ds Course Hero
· The problem is I have to find all the possible combination of integers (x, y, z) that will satisfy the equation x^2 y^2 z^2 = N when you are given an integer N You have to find all the unique tuples (x, y, z) For example, if one of the tuple isConsider f x y z xyze x 2 y 2 z 2 a Find the critical points of f b Show that from MATH 237 at University of WaterlooZ 2 2 x 2 x 2 y 2 z 2 2 x 2 y 2 z 2 Using this as a pattern we see that F x 2 y from MAT 21d at University of California, Davis



Solved Select The Domain Of The Given Function 12 Yz F X Chegg Com



Solved Problem 1 12 Points Let F X Y X2 Y2 A F Chegg Com
Question Find the ordered triple of these equations x y z = 16 x z = 12Y Simplify —— x 2 Equation at the end of step 1 y (((((x 2)(y 2))(z 2))(2x•——))y 2)z 2)2xz x 2 Step 2 Rewriting the whole as an Equivalent Fraction 21 Subtracting a fraction from a whole Rewrite the whole as a fraction using x as the denominatorPlot f (x,y,z)=x^2y^2z^2 WolframAlpha Assuming "plot" is a plotting function Use as referring to geometry instead
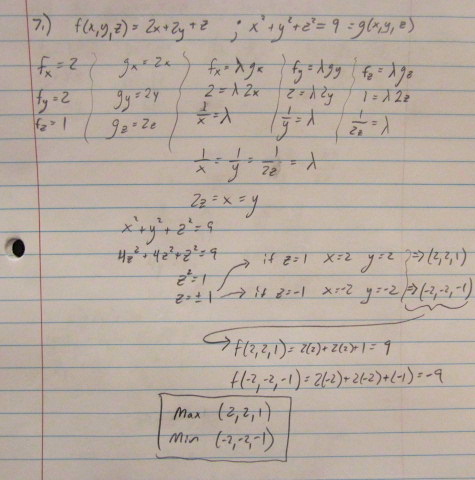


Use Lagrange Multipliers To Find The Maximum And Minimum Values Of The Function Subject To The Given Constraint F X Y Z 2x 2y Z X 2 Y 2 Z 2 9 Homework Help And Answers Slader



1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download
· Sadece x ve y değişkenleri ile sorulmuş olsaydı çözebilirdim sürekli olduğunu gösterme tanımından ancak z olunca kitlendim ( 8, Aralık, 15 komkesersedat ( 24 puan) tarafından yorumlandı · Verify GDT for vector F = (x2 yz)vector i (y2 zx)j (z2 xy)k taken over the rectangular parallelepiped 0 ≤x ≤ a, 0 ≤ y ≤ b, 0 ≤ z ≤ c vector calculus Share It OnUsing the theory of elliptic curves, we study the nontrivial rational (parametric) solutions of the Diophantine equations z2 =f(x)2±f(y)2 z 2 = f ( x) 2 ± f ( y) 2 for some simple Laurent polynomials f(x) f ( x)



If X 2 Y 2 Z 2 R 2 And X Y Z 0 Then Tan 1 Xy Z
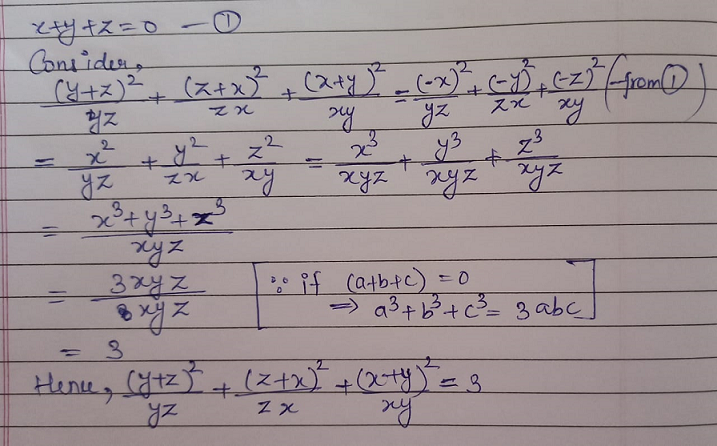


How To Solve If X Y Z 0 Find The Value Of Y Z 2 Yz Z X 2 Zx X Y 2 Xy Mathematics Topperlearning Com 7bcu50oo
Click here👆to get an answer to your question ️ If u = f(r) , where r^2 = x^2 y^2 z^2 , then prove that ∂^2u∂x^2 ∂^2u∂y^2 ∂^2u∂z^2 = f^\" (r) 2rf (r)Answer to Let f(x,y,z)=x^2y^2z^2 and let S be the level surface defined by f(x,y,z) = 4 (a) Find an equation for the plane tangent to SGraph the surface f (x,y,z) = c I have a function f (x,y,z) = x^2 y^2 z^2 and I'd like to graph the surface defined by the equation f (x,y,z) = 1 When I type "S x^2 y^2 z^2 = 1" into the input bar, this works perfectly;



Solved 2 Find The Maximum Value Ofthe Function F X Y Z Chegg Com



17 Given F X Y Z X Yz Xyz P 2 1 1 And Vector V 1 0 1 Find Homeworklib
F (x) = (x y z) {x 2 − (y z) x (y 2 − y z z 2)} = (x y z) (x 2 y 2 z 2 − x y − y z − z x) ホーム>>カテゴリー別分類>>数と式>>整式:因数分解の公式 (xyz)(x^2y^2z^2xyyzzx) 最終更新日: 14年9月9日$ x y z = 12 \ $ and $\ x^2 y^2 z^2 = 12 $ Normally these questions have a simple and elegant solution and although I've managed to solve it, the answer I found was neither!6 ( points) Let f(x;y;z) = x2 y2 z2 Find all solutions (x;y;z) of the system of equations coming from minimizing f(x;y;z) subject to the constraint yz x3 3 = 1 using the method of Lagrange multipliers Then nd the point (or points) where the minimum happens and write what that minimum value is Let g(x;y;z) = yz x3 3


If X 2 Y 2 Z 2 2 X Y Z 3 What Is The Value Of 2x 3y 4z Quora
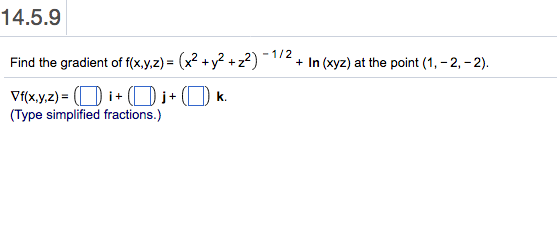


Solved Find The Gradient Of F X Y Z X 2 Y 2 Z 2 Chegg Com
I wondered if anyone can see a simpler way to tackle the problem The way I solved this was to use the first equation to eliminate $z$ in the second question I then factorised the resulting equation to obtain $(x12)(yAnswer to Evaluate the triple integral of f(x, y, z) = z(x^2 y^2 z^2)^{\frac{3}{2}} over the part of the ball x^2 y^2 z^2 \leq 49X 2 y 2 = z 2 Subtract x^ {2} from both sides Subtract x 2 from both sides y^ {2}=z^ {2}x^ {2} y 2 = z 2 − x 2 Take the square root of both sides of the equation Take the square root of both sides of the equation y=\sqrt {\left (zx\right)\left (xz\right)} y=\sqrt {\left (zx\right)\left (xz\right)}



How To Factorise Math Yz 2 Xz 2 Y 2z X 2y X 2z Xy 2 2xyz Math Quora



Math 6c Chapter 12 Quiz
If F = ( x 2, y 2, z 2), S = { x 2 y 2 z 2 = 1, z ≥ 0 }, evaluate ∬ S F d S I'm having trouble computing this In spherical coordinates we get which is really hard to evaluate But we know that the normal vector to the sphere is r = ( x, y, z), hence, Can we say that the first summand evaluates to zero since S is symmetrical with respect to3dprinting, solidworks f(0,0,0) is 0, not 1 (the isosurface level), so you only get points drawn completing the cones if there are enough points near the origin that happen to have value 1 But when you switch to linspace(,,), the closest coordinates to the origin are at about 105, leaving a gap of about 21If Y is the Mean Proportional Between X and Z Prove that (X^2 Y^2 Z^2)/(X^(2) Y^(2) Z^(2)) = Y^4 Chapter 7 Ratio and Proportion (Including



Answered 9 M A Y Z Xyz Xyz P 2 1 1 U Bartleby



Let X Y Z Be Real Numbers Satisfying X Y Z 3 X 2 Y 2 Z 2 5 And



17 Given F X Y Z X Yz Xyz P 2 1 1 And Vector V 1 0 1 Find Homeworklib


What Are The Maximum And Minimum Values Of A Point 3 4 12 From The Sphere X 2 Y 2 Z 2 1 Using The Lagrange Method Quora
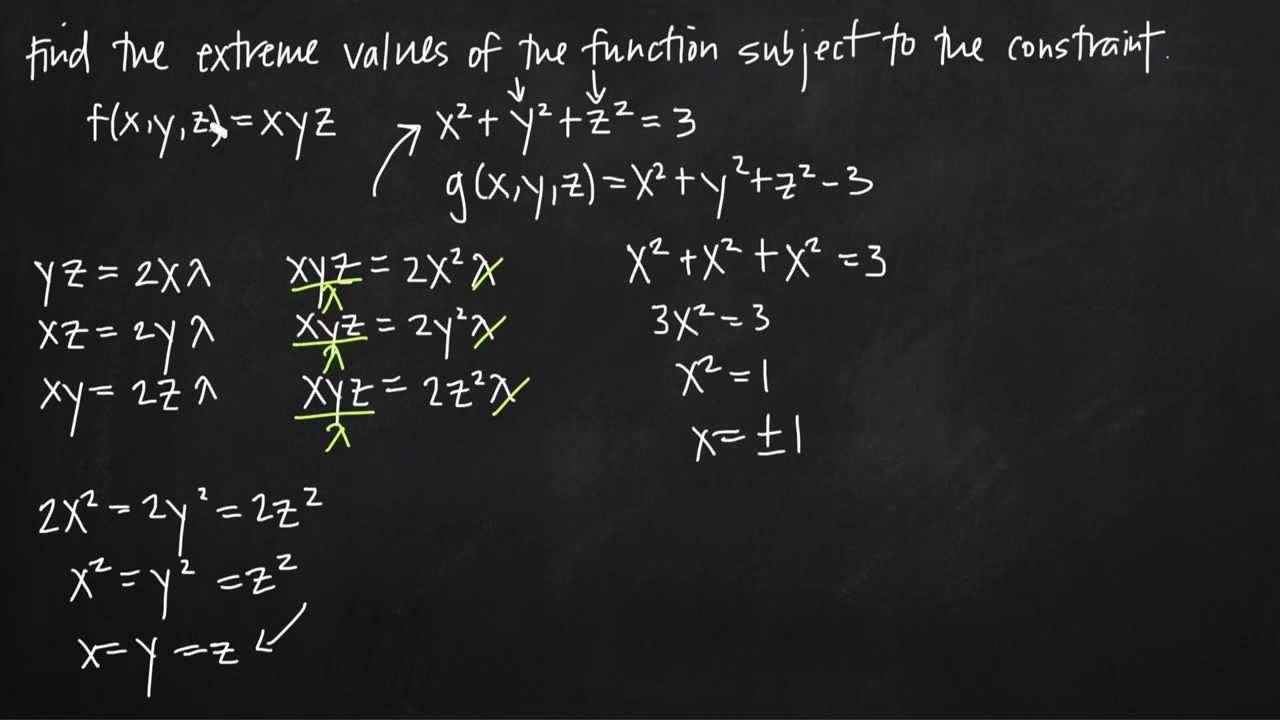


Lagrange Multipliers Three Dimensions One Constraint Kristakingmath Youtube



Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx Youtube



Example 15 If X Y Z Are Different Show 1 Xyz 0 Class 12



Solved Let F X Y Z X 2 2yz 2 Xyz And G X Y Z Chegg Com



Let F Xyz X21 Xy K Evaluate T See How To Solve It At Qanda



X Y Z Ds For The Following A F X Y Z X 4 Where S Is The Portion Of The Generalized Cy Homeworklib



Level Surfaces



Boolean Simplification I Have Noted That In Rows 2 And 7 There Is An Additional Term Added Which Already Appears In The Same Row For Example Row 2 Xyz Xyz


Find The Minimum Value Of X 2 Y 2 Z 2 Subject To The Conditions Xy Yz Zx 3a 2 Sarthaks Econnect Largest Online Education Community



Integrate F X Y Z xz Over The Region In The First Octant X Y Z 0 Above The Parabolic Cylinder Brainly Com



X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In



Example 14 Divide 24 X 2yz Xy 2z Xyz 2 By 8xyz Using Both



Consider Minimizing And Or Maximizing A Function Z F X Y Subject To A Constraint G X Y C Y Z X Z F X Y Parametrize The Curve Defined By G X Y Ppt Download



Solved 12 For The Function F X Y Z X Y2 Z2 25 Desc Chegg Com


Lagrange Multipliers Maximum Of F X Y Z Xyz Subject To X Y Z 3 0 Youtube



Teorema De Lagrange



Answered 12 The Function F X Y Z Xyz 1 2 Bartleby
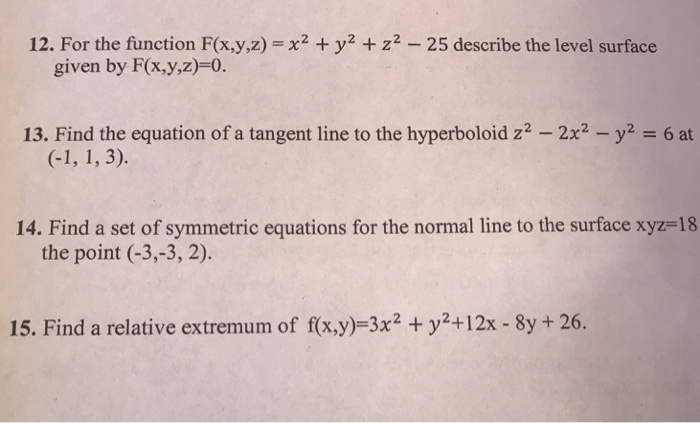


Solved 12 For The Function F X Y Z X Y2 Z2 25 Desc Chegg Com



14 8 Lagrange Multipliers Ppt Download



Multiplicadores De Lagrange Maxima And Minima Space



Solved Find The Differential Of F X Xyz X Y Z Find Chegg Com


Using Properties Of Determinants Prove That X Y Z X 2 Y 2 Z 2 X 3 Y 3 Z 3 Xyz X Y Y Z Z X Sarthaks Econnect Largest Online Education Community


Solved Use Lagrange Multipliers To Find The Indicated Ext Chegg Com



If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz Youtube



Prove The Following Using Properties Of Determinants X Y Z
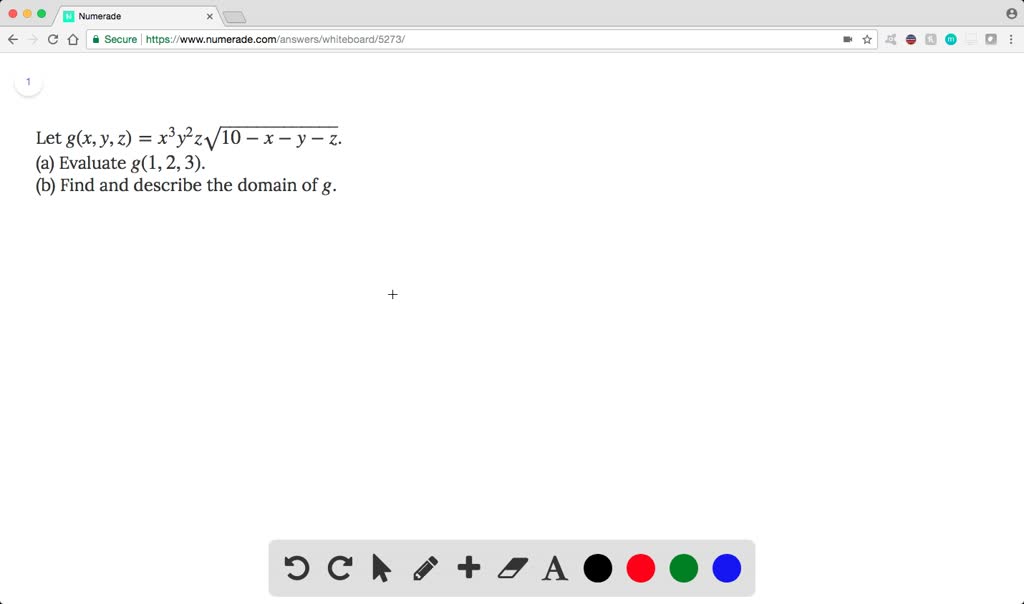


Solved Let G X Y Z X 3y 2z Sqrt 10 X Y



Rectangular Parallelepiped Of Greatest Volume For A Given Surface Area S Mathematics Stack Exchange
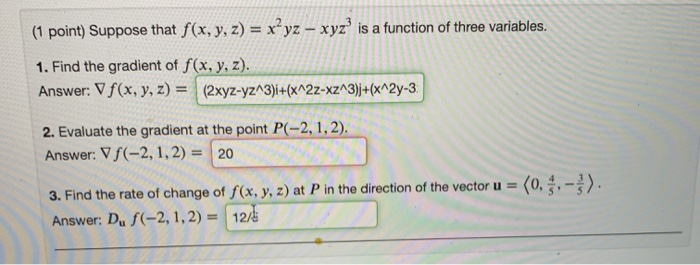


Solved 1 Point Suppose That F X Y Z X Yz Xyz Is Chegg Com



If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3 Youtube
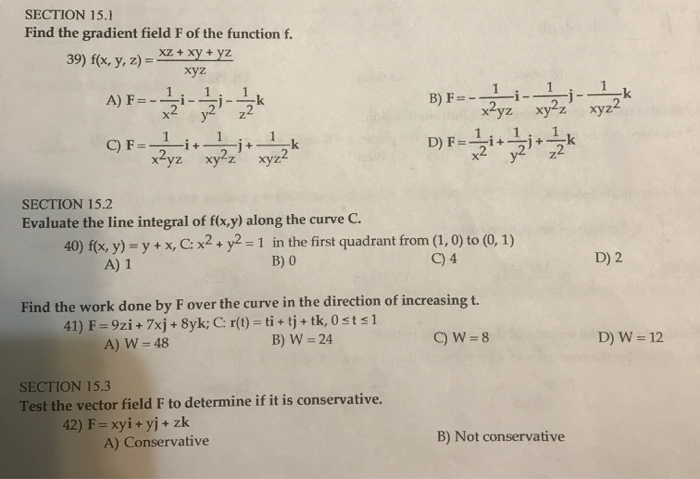


Solved Section 15 1 Find The Gradient Field F Of The Func Chegg Com


Solved 6 Find The Maximum Value Of The Function F X Y Z Xyz On The Sphere X2 Y2 Z2 12 8 4 0 4 8 None Of These Rm 9 0 9 S 7 Maximi Course Hero



Solved 7 F X Y X Y P 2 1 8 F X Y X In Y P 3 Chegg Com



Solved For The Function F X Y Z X 2y Y 2z Z 2x Chegg Com


Using Properties Of Determinants Prove That Y X 2 Xy Zx Xy X Z 2 Yz Xz Yz X Y 2 2xyz X Y Z 3 Sarthaks Econnect Largest Online Education Community
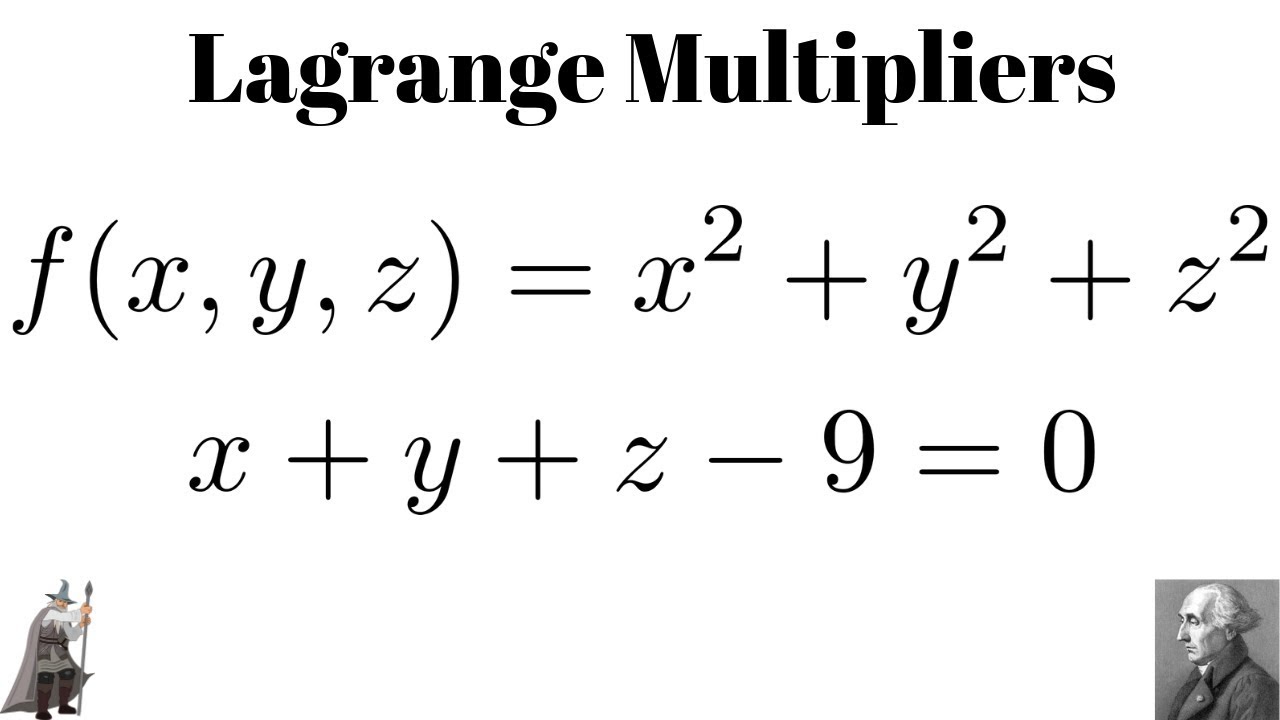


Lagrange Multipliers Minimum Of F X Y Z X 2 Y 2 Z 2 Subject To X Y Z 9 0 Youtube



Solve Equations X Y Z 1 2x 2y 3z 6 X 4y 9z 3 By Using Cramers Rule Answer Is 7 10 4 Brainly In



Solved 1 F X Y X2 Xyz Z Find Fxzy At 1 1 1 A 2 Chegg Com



Answered 12 Let G X Y Z X Y Z 10 X Y Bartleby



Solutions To Assignment 7


Surface Area


If A X B B Y C C Z A What Is Xyz Quora
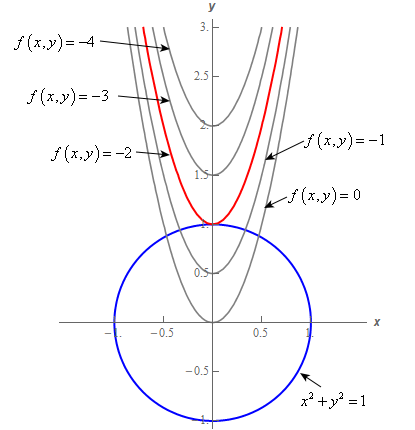


Calculus Iii Lagrange Multipliers



Example 32 Show That Determinant 2xyz X Y Z 3 Class 12



Level Surfaces


If Xyz 1 Then How Can I Prove That Math 1 X Y 1 1 1 Y Z 1 1 1 Z X 1 1 1 Math Quora



Lagrange Multipliers By Rohit Venkat Ppt Video Online Download



Btech Ii Engineering Mathematics Unit4
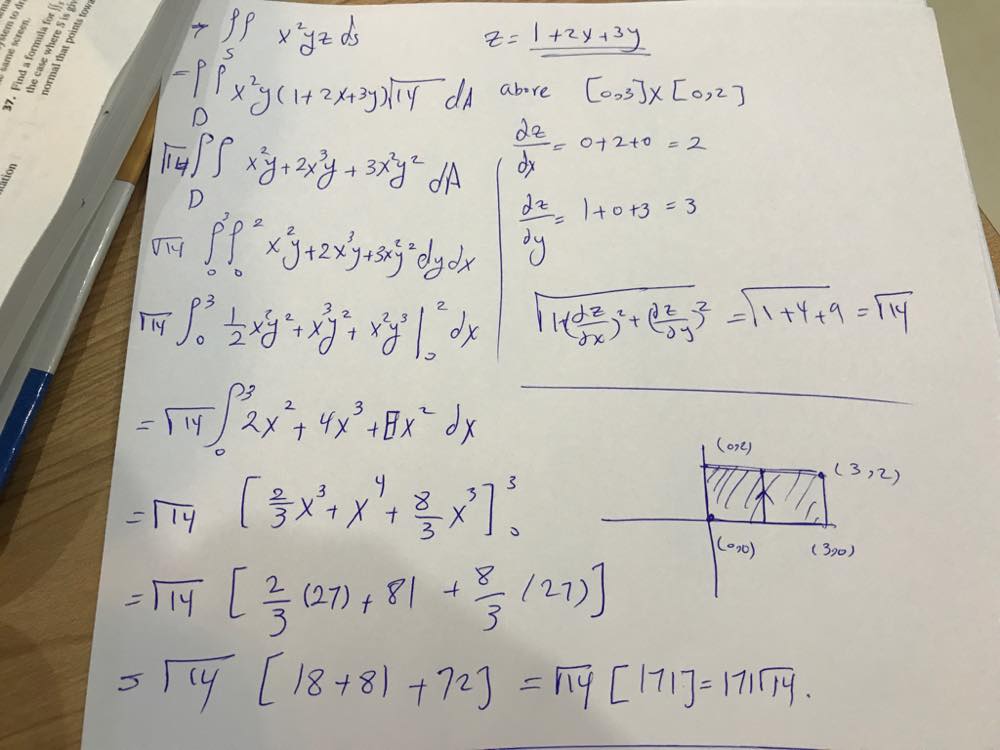


Evaluate The Surface Integral Double Integral X 2yz Ds S Is The Part Of The Plane 2x 2y Z 4 That Lies In The First Octant Homework Help And Answers Slader


Find The Product 1 X Y Z X2 Y2 Z2 Xy Yz Zx 4 Gr Scholr



If 3x 4y 12z Then What Is X Y Z Quora


Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline



Satyabama Niversity Questions In Vector



Graphing A Plane On The Xyz Coordinate System Using Traces Youtube



Document



Calc3 1001 By James Bardo Issuu
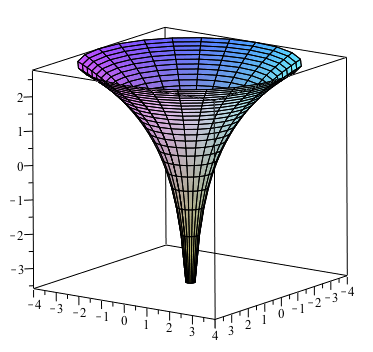


How Do You Sketch F X Y Ln X 2 Y 2 Socratic


